[번역] 전치 합성곱을 사용한 업샘플링(Up-sampling with Transposed Convolution)
출처 : https://kikaben.com/up-sampling-with-transposed-convolution/
참고용 깃허브 : https://github.com/naokishibuya/deep-learning/blob/master/python/transposed_convolution.ipynb
자료 제목 :Up-sampling with Transposed Convolution
Gentle Reminder : 번역 중 중심내용은 되도록 직역, 아닌 부분은 가독성을 위해 의역을 사용하였습니다. 정확한 내용은 위 출처 원문에서 확인 가능합니다. 아래 글은 영문 원문 읽기 전 참고용으로만 사용하기를 권장드립니다.
Up-sampling with Transposed Convolution
게재일 2017년 11월 13일
전치 합성곱에 대해 들어보았지만 아직 개념이 헷갈린다면 아래 글을 읽어보기를 바랍니다.
📌목차
- 업샘플링이 필요한 이유(The Need for Up-sampling)
- 왜 전치 합성곱을 사용할까?(Why Transposed Convolution?)
- 합성곱 연산(Convolution Operation)
- 역으로 가기(Going Backward)
- 합성곱 행렬(Convolution Matrix)
- 전치 합성곱 행렬(Transposed Convolution Matrix)
- 요약
1. 업샘플링이 필요한 이유
신경망을 사용하여 이미지를 생성할 때는 보통 저해상도에서 고해상도로 업샘플링을 수행해야 합니다.

업샘플링을 수행하는 다양한 방법이 있습니다:
- 최근접 이웃 보간법 (Nearest neighbor interpolation)
- 바이리니어 보간법 (Bi-linear interpolation)
- 바이큐빅 보간법 (Bi-cubic interpolation)
이 모든 방법은 네트워크 아키텍처를 결정할 때 우리가 선택해야 하는 보간법을 포함합니다.
이는 수동적인 특징 공학과 비슷하며, 네트워크가 학습할 수 있는 여지는 없습니다.
2. 왜 전치 합성곱(Transposed Convolution)을 사용할까?
네트워크가 최적으로 업샘플링을 학습하도록 하려면 전치 합성곱을 사용할 수 있습니다.
이는 미리 정의된 보간법을 사용하지 않고, 학습 가능한 매개변수를 가지고 있습니다.
전치 합성곱 개념을 이해하는 것은 중요한 논문과 프로젝트에서 유용합니다.
예를 들어:
- DCGAN의 생성자는 임의로 샘플링된 값을 사용하여 전체 크기의 이미지를 생성합니다.
- 시맨틱 분할(semantic segmentation)에서 인코더는 합성곱 계층을 사용하여 특징을 추출하고, 디코더는 원본 이미지 크기로 복원하여 원본 이미지의 각 픽셀을 분류합니다.
참고로 전치 합성곱은 Fractionally-strided convolution 또는 Deconvolution(역합성곱)이라고도 불립니다.
이 글에서는 전치 합성곱이라고만 부르지만, 다른 글에서는 대체 명칭을 볼 수 있습니다.
3. 합성곱 연산(Convolution Operation)
합성곱 연산이 어떻게 작동하는지 간단한 예시를 통해 설명하겠습니다.
4x4 행렬이 있고, 3x3 커널을 사용해 패딩 없이 스트라이드 1로 합성곱 연산을 적용한다고 가정해 봅시다.
아래에 나온 것처럼 출력은 2x2 행렬입니다.

합성곱 연산은 입력과 커널 행렬 사이의 요소별 곱의 합을 계산합니다.
우리는 패딩 없이 스트라이드 1을 사용하므로 이 계산을 4번만 수행할 수 있습니다. 따라서 출력 행렬은 2x2입니다.

이러한 합성곱 연산의 중요한 점은 입력 값과 출력 값 사이에 위치적 연결성이 존재한다는 것입니다.
예를 들어,
입력 행렬의 좌측 상단 값은 출력 행렬의 좌측 상단 값에 영향을 미칩니다.
3x3 커널을 사용하여 9개의 입력 행렬 값을 하나의 출력 값에 연결합니다. 합성곱 연산은 다대일 관계를 형성합니다.
이 점을 기억해 두면 이후에 유용하게 쓰입니다.
4. 역으로 가기(Going Backward)
이제 역방향으로 가고 싶다고 가정해 봅시다. 한 행렬의 하나의 값을 다른 행렬의 9개의 값에 연결하고자 합니다. 이는 일대다 관계이며, 합성곱 연산을 역으로 수행하는 것과 같습니다. 이것이 전치 합성곱의 핵심 아이디어입니다.
예를 들어, 2x2 행렬을 4x4 행렬로 업샘플링합니다. 이 연산은 1대 9의 관계를 유지합니다.
하지만 어떻게 이런 연산을 수행할까요?
이를 설명하기 위해서는 합성곱 행렬과 전치 합성곱 행렬을 정의해야 합니다.
5. 합성곱 행렬(Convolution Matrix)
합성곱 연산을 행렬로 표현할 수 있습니다.
이는 커널 행렬을 재배열하여 행렬 곱셈으로 합성곱 연산을 수행할 수 있게 하는 방식입니다.

예를 들어, 위와 같은 3x3 커널을 4x16 행렬로 재배열하면 아래와 같습니다.

이것이 합성곱 행렬입니다.
각 행은 하나의 합성곱 연산을 정의합니다.
잘 이해되지 않으면, 아래 다이어그램이 도움이 될 수 있습니다.
합성곱 행렬의 각 행은 다른 위치에 0 패딩이 있는 커널 행렬을 재배열한 것입니다.
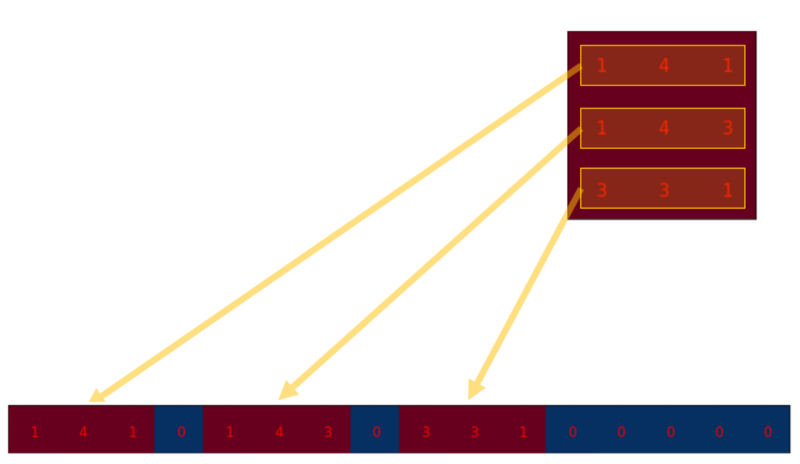
이 행렬을 사용하려면, 아래와 같이 입력 행렬(4x4)을 열 벡터(16x1)로 평탄화(flatten) 해야 합니다.
그다음 4x16 합성곱 행렬과 16x1 입력 행렬(16차원 열 벡터)을 행렬 곱셈합니다.

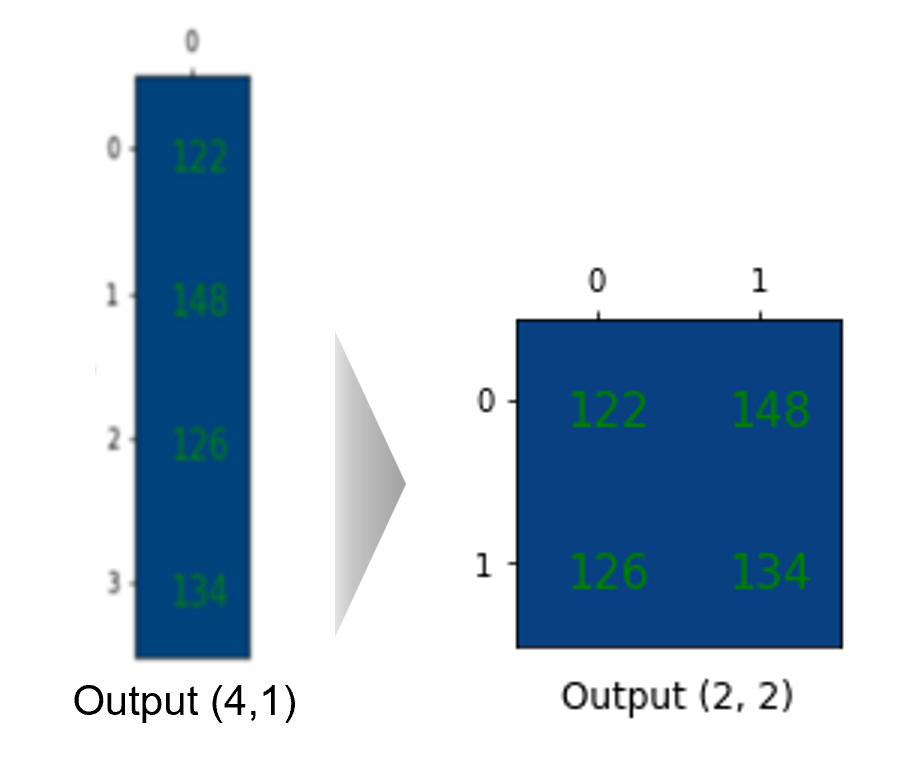
이렇게 출력된 4x1 행렬은 2x2 행렬로 재구성할 수 있으며, 이는 동일한 결과를 제공합니다.
이것이 가능한 이유는,
합성곱 행렬은 재배열된 커널 가중치일 뿐이며, 합성곱 연산은 합성곱 행렬로 표현하기 때문입니다.
위의 말을 다른 식으로 말해보자면,
합성곱 행렬이 4x16일 때 합성곱 행렬을 사용하면 16(4x4)에서 4(2x2)로 변환할 수 있고,
반대로 만약 행렬이 16x4이라 4(2x2)에서 16(4x4)으로 갈 수 있다는 것입니다.
무슨 말이냐고요? 당황하지 마세요.
아래에서 다시 설명해 보겠습니다.
6. 전치 합성곱 행렬(Transposed Convolution Matrix)
만약 4(2x2)에서 16(4x4)으로 변환하고 싶다면, 우리는 16x4 행렬을 사용합니다. 여기서 중요한 것은 1대 9 관계를 유지해야 한다는 것입니다.
합성곱 행렬 C(4x16)를 전치(C.T)하여 C.T(16x4)를 만들고, 열 벡터(4x1)와 행렬 곱셈하여 출력 행렬(16x1)을 생성할 수 있습니다. 전치된 행렬은 하나의 값을 출력에서 9개의 값에 연결합니다.

출력은 4x4로 재구성할 수 있습니다.

이로써 작은 행렬(2x2)을 더 큰 행렬(4x4)로 업샘플링했습니다.
전치 합성곱은 가중치 배치를 통해 1대9 관계를 유지합니다.
참고로, 실제 가중치 값은 원래 합성곱 행렬에서 오지 않습니다.
중요한 것은 가중치 배치가 전치된 합성곱 행렬의 모양과 동일하게 배열된다는 점입니다.
7. 요약
전치 합성곱 연산은 일반적인 합성곱과 동일한 연결성을 형성하지만, 방향만 반대입니다.
이 방법을 사용하여 업샘플링을 수행할 수 있습니다.
게다가 전치 합성곱의 가중치는 학습 가능합니다.
그래서 미리 정의된 보간법이 필요 없습니다.
전치 합성곱이라고 해서 기존 합성곱 행렬을 가져와서 전치된 버전을 사용한다는 뜻은 아닙니다.
중요한 것은 입력과 출력 사이의 연결이 일반적인 합성곱 행렬과는 반대로 처리된다는 점입니다(일대다 관계, 일반 합성곱의 다대일 관계와 반대).
따라서 전치 합성곱은 합성곱이 아닙니다만 전치 합성곱을 합성곱으로 에뮬레이션 할 수 있습니다.
입력 행렬의 값 사이에 0을 추가하여 입력을 업샘플링한 후 합성곱을 수행하면 전치 합성곱과 동일한 효과를 낼 수 있습니다. 그러나 입력을 업샘플링하기 위해 0을 추가해야 하므로 비효율적입니다.
주의할 점: 전치 합성곱은 생성된 이미지에서 체커보드 아티팩트(체커보드 패턴)를 유발할 수 있습니다. 이러한 문제를 줄이기 위해 보간 방법(업샘플링 연산) 후에 합성곱 연산을 사용하는 것이 권장됩니다. 이미지에서 이러한 아티팩트 없이 생성하는 것이 목표라면 관련 논문을 읽어보는 것이 좋습니다.